Pada pembahasan ini akan diberikan 10 soal program linear beserta pembahasannya. Soal-soal tersebut mencakup latihan memodelkan soal cerita ke dalam kalimat matematika, menggambar daerah selesaian dan menentukan nilai optimum dengan menggunakan uji titik pojok dan garis selidik.
Selain itu, ada soal yang membahas mengenai kasus kusus dalam
permasalahan program linear, seperti titik pojok penyebab nilai optimum
yang koordinatnya memuat bilangan bukan cacah, akan tetapi fungsi
objektifnya mensyaratkan bilangan cacah. Berikut ini satu dari kesepuluh
soal tersebut.
Seorang pedagang sepeda ingin membeli 25 sepeda untuk persediaan. Ia
ingin membeli sepeda gunung dengan harga Rp 1.500.000,00 per buah dan
sepeda balap dengan harga Rp 2.000.000,00 per buah. Ia berencana tidak
akan mengeluarkan uang lebih dari Rp 42.000.000,00. Jika keuntungan
sebuah sepeda gunung Rp 500.000,00 dan sebuah sepeda balap Rp
600.000,00, maka keuntungan maksimum yang diterima pedagang adalah …
Pembahasan Tanpa membuat tabel, kita dapat memodelkan kendala-kendala dari permasalahan tersebut sebagai berikut.
x + y ≤ 25,
1.500.000x + 2.000.000y ≤ 42.000.000,
x ≥ 0, y ≥ 0,
x dan y bilangan cacah.
Dengan fungsi objektifnya adalah f(x, y) = 500.000x + 600.000y. Sehingga apabila digambarkan, daerah selesaiannya akan nampak seperti berikut.
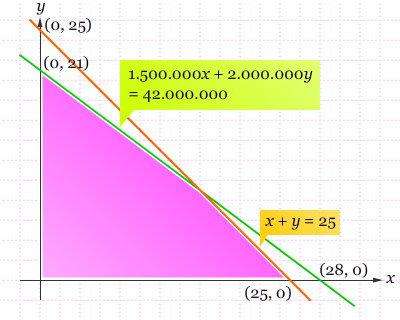
Selanjutnya kita tentukan titik potong grafik persamaan 1.500.000x + 2.000.000y = 42.000.000 dan x + y = 25.

Sehingga,
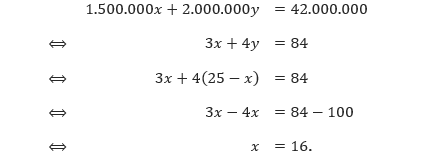
Diperoleh,
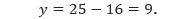
Selanjutnya kita lakukan uji titik pojok ke dalam fungsi objektifnya.
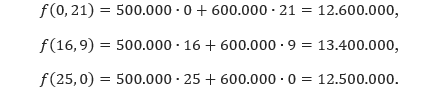
Jadi, keuntungan maksimum yang diterima pedagang adalah Rp 13.400.000,00.


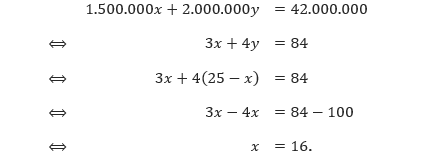
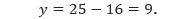
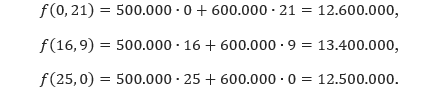
Tidak ada komentar:
Posting Komentar